Edge and circle detection

Edge detection is an important application of Image processing. As the name indicates the idea is to detect edges in an input image and to highlight them using image processing algorithms. Different methods exist today to detect edges and the most commonly used algorithm is Sobel edge detection. Sobel edge detection is a direct application of differential calculus. Circle detection is an extension of edge detection in which we aim to find circle-like edges in the input image. Hough transform is an important geometric method to find circles from edges in an image. In this article, we will discuss both the concepts and their implementation, both in gray-scale and color images.

Edge detection

As we know a digitized image is represented in a computer as an array of two-dimensional pixels. A pixel is the smallest unit inside an image that can be uniquely captured using the camera. The number of pixels in an image depends on the resolution capacity of the camera. In a grayscale image, each pixel corresponds to the intensity level in that particular pixel and its value ranges from zero to 255. In color images, each pixel has red, green, and blue color levels with values ranging from zero to 255. Theoretically, a mixture of these three colors can generate any visually identifiable colors of human perception.

In edge detection, our aim is to identify portions of the image where information is densely populated. This means we are interested in identifying those pixels which form edges in an image. Edges in the image are identified by comparing them with the pixel intensity of neighboring pixels. Larger the difference or variation in brightness of pixel values, the larger the likelihood that it is an edge pixel. Therefore our interest is to identify those pixels which significantly differ from their neighboring pixels. 

The application of calculus comes into play here. We know that calculus is the study of change just like geometry is the study of shapes. Assuming that the pixel values in an image form a discrete function, our aim is to find the points in the discrete function whose slope is higher. Since an image is a 2-D function, operators describing edges can be expressed by using partial differential equations. The points that lie on an edge can be detected by detecting the local maxima or minima of the first derivative or by detecting zero-crossing of the second derivative. The idea is described in figure (1) for 1-D analysis. However, since noise in an image often forms pseudo-edges we have to pre-process the image. Therefore edge detection can be described in four steps as below.

(a)   Smoothing – to reduce noise without destroying true edges
(b)   Enhancement – improve the quality of the edges (eg. by improving sharpness)
(c)   Detection: find the edge pixels
(d)   Localization: find the exact location of the edge. (eg. linking edges together)

Figure (1) - Idea of edge detection in 1-D intensity signal function. Changes in edge can be detected using local maxima or minima of the first derivative or using the zero-crossing in the second derivative. (Source here)

The derivative of a 1-D signal can be computed by approximating the derivative by finite differences. 

Therefore








Mask for 1D signal: [-1 0 1] (centered about x)

Computing the second derivative gives,









Mask for 1-D signal using second derivative: [1 -2 1] (centered about x)

Based on the 1-D theoretical analysis, the same idea can be extended to two-dimensional pixel planes, and one such extension is known as the Sobel operator. The Sobel operator performs an accurate approximation to calculate the derivative of a two-dimensional image by computing the spatial gradient measurement of an image. Sobel detector uses a pair of 3 x 3 convolution masks, one for x-direction and the other for y-direction. Sobel operator for a two-dimensional image is as follows and it slides over the image.

Figure (2) – Sobel operator for edge detection in images.

The magnitude of the gradient is calculated using the resultant formula:

The direction is calculated by using the inverse tangent of the gradients in each direction.

.

Figure (3) – Gradient edge and direction (source)

Some of the results of applying the Sobel operator in grayscale images and color images are shown below. In color images, we compute the intensity and use it for edge detection.

Intensity  I = (red + green + blue) / 3

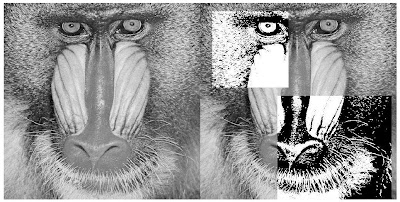
After computing the edges, thresholding is applied to highlight edges that are highly likely. Again we can highlight those edges which are in a particular direction by thresholding edge intensity image using computed direction information.

Figure (4) Original Image, Edge image, Thresholded edge image and direction thresholded edge image (clockwise). ROI (x,y,sx,sy) = (10,10,450,620), threshold value = 80 and direction threshold value = 80 to 90 degrees.

Figure (5) Original Image, Edge image, Thresholded edge image and direction thresholded edge image. The ROI (x,y,sx,sy) = (10,10,450,620), threshold value = 80 and direction threshold value = 70 +- 10  degrees.

Figure (6) Original Image, Edge image, Thresholded edge image and direction thresholded edge image. The ROI (x,y,sx,sy) = (10,10,550,550), threshold value = 80 and direction threshold value = 45 +- 10 degrees.

Circle detection using Hough transform

Circle detection in image processing is done using Hough transform. Hough transform is a feature extraction technique to find imperfect instances of objects within a certain class or shape. This is done by parameterization and then voting the parameter space to find local maxima. First, we compute the edges of the image using edge detection. Then we threshold the edge image so that we can find significant edges. Now we have to find those edges which form a circle. Note that after edge detection circumference of the circles might not be connected clearly. So we apply Hough transform.

A circle can be described completely with three pieces of information: the center (a, b) and the radius R.

x = a + Rcosθ
y = b + Rsinθ

When the θ varies from 0 to 360, a complete circle of radius R is generated. We note that for a circle the parameters (a, b, R) are constant. In the parameter space, we plot the coordinates with (a, b) boundary equivalent to the set of all possible centers in a given image where θ ranges from 0 to 360. For each edge point that correspond to (x, y, R) of a particular circle in real space we draw the sphere in the corresponding (a, b, R) parameter space. If we are looking for circles of a particular radius R then we have a 2D parameter space. 

Figure (7) – Each point in the geometric space (left) generates a circle in parameter space (right). The circles in the parameter space intersect at (a,b) the center of the circle in geometric space. (source)

Rearranging the equations we get

a = x₁ – Rcosθ

b = y₁ – Rsinθ

After plotting the circles in parameter space, we will note that the points at which circles in parameter space intersect correspond to the center of the circle in real space. To find circles that are more likely true we compute intersections that have a high density. This is done by sampling the parameter space with a suitable bin size. Once we compute the local maxima we highlight the circle in the original space. Some results for both greyscale and color images are shown below.

Figure (8) Original Image, Edge image, Thresholded edge image, PSpace image and Resulted circle. The ROI (x,y,sx,sy) = (10,10,300,300), threshold value = 80 and radius = 33 px.

Figure (10) Original Image, Edge image, Thresholded edge image, PSpace image and Resulted circle. The ROIs (x,y,sx,sy) = (110 10 200 200)(110 280 200 200), threshold value = 80 and radius = 90 px.

Figure (11) Original Image, Edge image, Thresholded edge image, PSpace image and Resulted circles. The ROIs (x,y,sx,sy) = (180 220 80 80) (180 320 80 80), threshold value = 80 and radius = 11 px.

I have included sample code in c++ for edge detection and Hough transform. Code for classes ROI, Images are excluded.

I posted my code used in this article in Git.

Histogram Equalization

A histogram is a graphical representation of the tonal values of an image. In a greyscale image, we have only one channel, and its value range from 0 to 255. Based on the number of pixels falling under a particular tonal value we plot the histogram graph. 

Grey histogram Equalization

In Grey histogram equalization we enhance the contrast of images by using usable pixel values in the image to the close contrast values of the display device. This is accomplished by spreading out the most frequent intensity values to the neighboring intensities. First, we compute the cumulative distributive function of the histogram. Then we use the general histogram formula to accomplish this.

The general histogram equalization formula is:

Where cdf_min is the minimum value of the cumulative distribution function, M × N gives the image's number of pixels and L is the number of grey levels used. Some sample results are shown below. Note that equalization is done within the two regions of interest.

(a)   Original Image

(b)   Histogram for ROI 1 before and after equalization ( x = 10, y = 10, sx = 300, sy = 300)

(c)    Histogram for ROI 2 before and after equalization ( x =315, y =315, sx = 400, sy = 400)

(d) Result - equalized image

Color Histogram Generation (RGB)

In color images, we have three channels namely red, green and blue. Therefore in order to generate the histograms, we apply the same principle for greyscale images separately for each channel.

Color Histogram Equalization (RGB)

In color histogram normalization we apply the same method used for grey-scale equalization for each of the three channels separately. The results are shown below.

(a)   Original Image

(b) Histogram for ROI 1 – Before and after equalization - RGB ( x = 10, y = 10, sx = 300, sy = 300)

(c)   Result - equalized image (all channels together)

(d)   Equalization separately - Original and  RGB channels respectively (Clockwise)

               

HSI histogram generation

HSI is a color model which is more intuitive and perceptually relevant to co-ordinate space. It has wide applications in the field of computer graphics and vision. Like RGB it has three channels namely Hue (H), Saturation(S), and Intensity (I). Hue falls from 0 to 360 degrees, and the other two fall from 0 to 1. For the sake of calculations, we make saturation fall between 0 to 99 and Intensity fall from 0 to 255 respectively. For HSI histogram generation we need to convert the RGB color model to HSI. We then generate a histogram for the three channels separately. The formula for HSI to RGB and from RGB to HSI is below from the Gonzales and Woods text.

HSI histogram equalization

After generating HSI histogram we then compute the equalized histogram from it. For that, we make use of the same histogram formula we used before. After equalization, we then convert it back to RGB image for display. The resulted images are shown below.

(a)   HSI histogram for I channel – Before and after equalization (x = 10, y =10, sx = 300, sy = 300)

(b)    HSI equalization (original and I channel respectively)

Program

Some of the functions I used to do the above operations in C++ are in Git here. Note that the custom class Image and ROI are not included here. However, this code is enough for explaining the main logic.

Image thresholding and smoothing

Thresholding helps to visualize the useful portion of the image, whereas smoothing helps to remove noise from the image.  The images captured through a camera are generally in analog format and therefore it is digitized by sampling. The digitized image is stored in a computer in the form of pixel arrays. Each pixel contains information such as the color or intensity of that portion of the image. Pixel size depends on the sample size of the digitization process. In image thresholding, each pixel value is either set to black or white depending on a user-defined threshold value. In smoothing the pixel values are set based on the values of the neighboring pixels.

Image Scaling in Grayscale images

Image scaling is the process of incrementing the pixel values based on the user-defined scaling factor. Image scaling helps to increase the brightness of the image. In greyscale image scaling the user-defined value is added to the pixel value. Below is the image scaling result with a scaling factor 25, 50 in the Region of interest (ROI) one and two respectively. The brightness and hence the quality of the image are increased by scaling. The original image is shown on the left side and the scaled image on the right side.

Image thresholding in Grayscale images

Thresholding in the Grayscale images is done by setting the pixel values to 0 or 256 based on a threshold value defined by the user. For example, if the threshold value is 125 then all pixel values below 125 are set to 0 and all pixel values above 125 are set to 256. In this way, the image features are more easily identifiable. Below is the image thresholding result on a greyscale image with thresholding values 100, 150 for ROI one and two respectively.

Image thresholding in Color Images

In color thresholding, the distance between the RGB pixels of the image with the user-defined color values is then compared with a user-defined threshold TC. If the distance falls below the threshold then those pixels are set to white and all other pixels are set to black. A sample result with RGB (25,25,25) with TC = 205 and TC = 100 for ROI one and two are shown below respectively.

Adaptive Weighted thresholding in Grayscale images

In normal thresholding, the parameter provided by the user affects the entire image. Hence it might give undesirable results in images that have wide variability in intensity. Adaptive weighted thresholding helps to overcome this issue by using a weight factor W which is compared with the mean of the pixels falling inside the odd-sized window with the current pixel as the center. The result of such thresholding with Window size 3, 5 and threshold factor 15, 20 on ROI one and two are shown below respectively.

One dimensional Smoothing in Grayscale Images

In one-dimensional smoothing, the pixel values are averaged along one dimension of the two-dimensional pixel plane. The result of one-dimensional smoothing in X and Y direction separately is shown below with windows size 3, 5 on ROI one and two respectively. The window size should be selected reasonably so that blurring is kept to the minimal level possible.

Two-dimensional Smoothing in Grayscale images

In two-dimensional smoothing, the mean of the whole window in the two-dimensional plane is used as the pixel value. The result of two-dimensional smoothing with window sizes 3 and 5 on ROIs one and two is shown below.

Program

Some of the functions I used to do the above operations in C++ are in Git here. Note that the custom class Image and ROI are not included here. However, this code is enough for explaining the main logic.

Comparing Wi-Fi performance using experiments

N.B: I am posting by revising something I wrote for school purposes. So it doesn't look like a blog article.

File downloading via HTTP is one of the common tasks we do on the internet. Delays in file download can be caused by factors such as propagation, processing, file size, and traffic on the network. Delays caused by propagation are unavoidable, and therefore our interest is to keep the other delay factors to the minimal level possible. In this paper, we design and conduct experiments from two public Wi-Fi spots to identify the effects of key factors that are perceived to be affecting the file download time over the internet. By doing so we explore if ping can be used to identify the file downloading time and the impact of location on file download time. From the results and analysis, we conclude on the comparative performance of the two Wi-Fi spots using statistical models.

INTRODUCTION

File downloading is a common task we do on the internet. The factors that affect the delay for file downloading include the traffic on the network, file size, time, and other related things. Nowadays Wireless Networks are made available free of cost at public places by many private business dealers in order to improve customer satisfaction. Such Wi-Fi hotspots are often jammed with a lot of users which may cause delays in file downloading.

In this paper, we perform experiments on two Wi-Fi spots, with a view to understanding the comparative performance with respect to File downloading. HTTP is a common internet protocol used for file retrieving. We compare the HTTP file downloading performance in two separate Wi-Fi hotspots at University Mall located near Tampa. A ping request is generally used by network administrators to check the status of remote servers. By default, a ping request sends a 32 byte ICMP packet to the server. The server, in turn, echoes back the same packet. Using the ping request thus we will be able to get an estimate of the total round trip time of the packet. In this paper, we also do experiments to understand if ping can be used to predict the file download time.

The related work section gives a brief overview of the research ongoing regarding the performance of file downloads. It is followed by the experimental setup and results. Finally, the results are analyzed and a conclusion is made.


RELATED WORK

File downloading performance has been a major field of research among network scientists in the past decade. Researchers have suggested that a slow start in TCP causes delays for small file downloads. Some researchers have suggested that the DNS causes delays in file download. The delay in downloading is caused by numerous factors which are hard to theoretically estimate. However, time of the day and file size is known to play a major role in deciding the file download time. Prefetching the file at the server was suggested by some researchers to improve the performance. It has been also suggested that the performance can be increased when the server rejects requests that exceed a threshold.

EXPERIMENTS

The experiment was conducted in two of the free Wi-Fi spot available at the University Mall\.

Setup

An HTTP server was set up at the ENB building on USF campus. The C based HTTP web server called Weblite, written by Dr. Ken Christensen at USF was used to do the experiment. A UNIX based Client was set up to request the file at the server through HTTP GET request. Two files with size 16 Kb, 484 Kb were respectively used to do the experiment. We assume these files as small and large based on some pre-experimental speed test on the location. Each experiment had 10 HTTP GET requests to send to the server. Once a request is finished the Client would wait for 100 milliseconds before sending the next request. In this way, ten experiments were done, with an interval of five seconds between each experiment. The experiment was done at two different Hot Spots at University mall, namely Food Court and Center Court. Experiments were conducted during peak traffic hours in noon and during fewer traffic hours at night. Each experiment has ten sample mean file download time. Ping time was also noted using command line tool during the experimentation and the average of random sample was used.

Results

The results of the experiments are tabulated in table one. It shows the Mean file download time for each of the eight scenarios along with the mean ping time for each experiment. The mean for each experiment is based on the sample download time during the experiment. Separate columns are shown based on the time of day and the file download size.

TABLE I. EXPERIMENT RESULTS

Comparison

We have the sample mean file download time for the 10 experiment done in the eight different scenarios. Now we would like to compare the results using confidence interval estimate. First, we determine the difference between sample means. Then we use T-scores to get the normal distribution. The result is shown in table 2.

TABLE II. COMPARATIVE RESULTS

We also checked if ping can predict the download time. As we know ping gives the total round trip time for 32 bytes of data. Using the mean ping time for random samples in table one, we can calculate the estimated download time by multiplying the one byte ping time with the file size. The result is shown in Table 3.


TABLE III. PING TIME

As we can see the ping can mostly predict the file download time for smaller files, however for larger files it’s not able to do so.

ANALYSIS

The reason for the variation in the file download time over the two locations is not so obvious from the results. Traffic in the network is likely to be one issue. In the food court, there were more people in the afternoon when compared to the center court. Similarly at night in the center room, there were more people than in the food court (since the food court was closed at night). The impact of file size is still not very clear, however as the average shows the large file download was slightly faster than the small file download. It could be the impact of the slow start in the TCP protocol. Similarly, the reason why ping is not able to predict large file download time is that of the packet loss observed during the ping experiment. It means that the link is not reliable for a long period of time where random delays occur due to unknown factors.

CONCLUSION

The experiments were conducted to compare the two public Wi-Fi spots. The results showed that one of the Wi-Fi was better than the other. Similarly, we showed that ping can predict the download time if the random delays during large file downloads can be avoided.

PROGRAM FOR EXPERIMENT

SQL injection prevention

This was a research project for software security coursework which I am sharing here on my blog.

SQL injection vulnerability was reported as a top cybersecurity issue in 2010 and is considered to be accounting for 10% of total cybersecurity vulnerabilities since 2002. It is a known fact that using parameterized queries can mitigate SQL injection vulnerabilities to a large extent. This paper shows the underlying practical issues programmers encounter when using parameterized queries. It also shows how a plugin tool inside the developer’s integrated development environment (IDE) could help programmers in generating parameterized queries. Further, the usefulness and practicality of this helping tool are discussed.

Introduction

SQL injection vulnerability (SQLIV) accounts for over 20% of input validation issues and 10% of the overall cybersecurity issues between 2002 and 2007. Further, it was reported as the second top cybersecurity vulnerability of the year 2010.  SQL injection vulnerability can lead to theft of confidential data, loss of money, loss of critical data, and affect the reputation of organizations.

Structured Query Language (SQL) is widely used as a standard method to interact with the relational databases from a webpage.  An SQL statement can call the database managing program, typically a database server to return a particular result set from the database table or to update the table. Typically SQL statements are not compiled until the request is made by the web page under execution. This is usually because the query would likely depend on user requests and may contain a user-entered input. An SQL injection happens when a malicious user persuades the user input in such a way that the developer-defined SQL query is modified undesirably. This is done by inserting code into the data part of the SQL query maliciously.

Several SQLIV mitigating mechanisms exist, of which the most effective one is the usage of a parameterized query, which is also known as prepared statements. Parameterized queries force the developer to define the code portion of the SQL query first and then clearly define the data portion of the query. In this way, the SQL compiler can safely distinguish between the code and the data portion of a query. It is interesting to note that parameterized queries were introduced a long period back; however, by contrast with the frequent occurrences of SQL injection attacks, we can conclude that they were not used by web developers, at least in some cases where attacks happened.

In this paper, we study the difficulties encountered in using parameterized queries. We developed a plugin tool namely SQLSecuritytool for Microsoft’s visual studio 2010 web development IDE that could aid web developers in ensuring the safety of SQL queries they use in server-side scripting. The findings, the practicality, and usefulness of this security tool are described in this paper. Section II discusses a brief background to understand this paper. Section III goes through the related work in mitigating SQL injection vulnerability. Section IV analyzes problems faced by web developers in using parameterized queries. Section V describes the tool we developed for replacing general SQL queries with parameterized queries. Finally, the security benefits and conclusion are discussed subsequently.

Background

This section gives some background about SQL Structure, SQL injection attacks, and parameterized queries.

SQL statement

An SQL statement defines the operations performed or requested to the database and is usually defined by a database analyst in consultation with the web developer. An example SQL query used in login pages is described below:

Select password FROM usernames_table WHERE username = ‘name’

The code portion of the above statement is shown below.

Select password FROM usernames_table WHERE username =

The data portion of the SQL query is ‘name’. Typically the data portion is known only at runtime. Therefore web developers substitute that field with a variable name. For example, in vb.net the above query would be defined by the web developer as shown in figure 1.

Figure 1.   Typical SQL query in a vb.net webpage server-side script

Password hashes obtained from the database are used to validate the username in this case.  Typically the database is connected by using the driver provided. In this case, Oracle client driver for asp.net is used which requires importing a dynamic link library (DLL) provided by Oracle company to the project.

SQL Injection Attack

An SQL injection attack happens when the developer fails to properly define his program in such a way so that there is always a desired separation between code and the data portion for any user inputs at runtime. Or by using standard definitions, an SQLIV is caused by dynamic SQL statement code combined with inadequately-verified input, which allows the input to change the structure and logic of an SQL statement.  For example, a user input “111’ OR true#“ would create the following query which would retrieve all passwords.

SELECT password FROM usernames_table WHERE username = ‘name’ OR true#’

If the web application is expected to display the results in a table then all the password hashes will be displayed to the attacker. In addition to this example, several other SQL injection methods exist. Fortunately, all of them work by mixing the user input with actual SQL code.

Parameterized query

Parameterized queries are SQL statements that take a static structure unaltered at runtime. It defines the user input as parameters expected at the runtime. Therefore it clearly makes a distinction between the code and the data portion of the SQL query. The query described in figure 1 can be changed to a parameterized query as figure 2 shows.

Figure 2.   Typical parameterized SQL query in a vb.net server-side script

There are multiple ways to define parameterized queries and it depends on the language in which the web developer programs. When a large SQL query is used a number of parameters may be required to be defined carefully.

Web development issues

It is generally known among web developers that using parameterized queries can give maximum security against SQL injection vulnerability. It is being suggested and encouraged as a standard pattern to be followed by web developers. However, if the existing code is not written using parameterized queries, it would be a tedious effort for the developer to walk through and carefully scrutinize the code to rewrite them using parameterized queries. Existing frameworks in dot net do not provide any help for migration to parameterized queries. Further in many organizations, the task of writing SQL statements are assigned to DB analyst. In small organizations, a developer may take the role of the DB analyst. This reason in addition to the time constraints may force those developers in writing their code in the easiest way, by not using any security mitigating logic such as parameterized queries. Personally, this reason and our knowledge of the dotnet framework gave me the motivation to write an automated tool to assist the developers.  

Replacement tool

The replacement tool I developed basically works as a plugin to the Microsoft Visual Studio IDE. Upon enabling this plugin and running, the developer is given options to find vulnerable SQL queries in the current project. Also, it provides the parameterized form of the vulnerable query so the developer can replace the vulnerable SQL code. The plugin works by using the Microsoft DTE interface which gives an object-oriented interface for developing plugin extensions to visual studio. The source code is analyzed using regular expressions. These two design components are discussed below.

DTE interface

Microsoft has exposed some of the inbuilt classes of the Visual Studio IDE to the developer through the DTE interface. The DTE object-oriented model allows the programmer to access the project, code, and other components of the visual studio from a user-defined plugin. Static analysis of the code is possible by using this interface. There are two ways to do static analysis. One is by analyzing the code components of the project using the DTE model which uses the inbuilt lexer and parser. Another is to use regular expressions to find the desired pattern of code. Each has its own pros and cons. The former can do static analysis accurately however it needs in-depth knowledge of the DTE object model. The latter is less accurate since we assume to have a lot of code patterns in the program. However, it is faster and easy to write. For the sake of this short academic project and also due to time constraints I opted to develop the tool using regular expressions.

Regular Expressions

Regular expressions provide a fast and easy way to make static analyses of the program code. It requires some basic understanding of creating a pattern which we want to match from code. Further many languages have an inbuilt regular expression engine that allows extracting text programmatically. We used the vb.net regular expression library provided by Microsoft. For example, the following expression could find the SQL statements occurring on vb.net server-side page.

SQL\s=\s.+?\n.*?(objcommand.\.CommandText\s=\sSQL|Me\.SqlDataSource.\.SelectCommand\s=\sSQL|ObjDataReader\s=\sobjcommand.ExecuteReader|objcommand\.CommandText\s=\sSQL)

Basically, it looks for text that matches the word SQL or obj command followed by the SQL query and execution commands. This pattern was able to detect many of the vulnerable codes in the project. The reason for this being a good pattern is that it exploits the common syntax used in vb.net programs to define SQL codes. However, it would not definitely give a perfect match, because the program can take a different structure depending on the developer's coding style. However with carefully scrutinized patterns, one could expect an average matching rate of around 70%.

Developer Interface

The developer user interface made use of the windows forms framework provided by Microsoft. It has various options to find the next occurrence of the unsecured SQL query in the project. If the matching code file which contains such an unsecured SQL query is not yet opened by the developer, it will be automatically opened. Further, the present unsecured SQL query found will be selected and highlighted in the code window. Further manual editing of the generated query can be done by modifying the suggested parameterized SQL query. The sample user interface screenshot is shown in figure 3.

Figure 3. User Interface

Assumptions and limitations

This conversion tool assumes that all command lines in the program are removed by the programmer before running the application. This is because the regular expressions could mismatch the comments as source code. Further, there are different ways to define the SQL code inside a program, but I assumed only the widely used syntax of defining SQL code in the source code. However, these issues can be avoided using the DTE code model with the inbuilt lexer and parser or by defining more scrutinized regular expression patterns. However, I believe it is out of scope for this short project.

Effectiveness

Since parameterized queries can guarantee protection against SQLIV the developed replacer tool is expected effective against most of the SQL injection vulnerability. We tested this tool against over ten different projects obtained from the internet and also from organizations. It showed a conversion rate of over 80% for those projects which used syntax similar to those defined in the regular expression pattern. Some of those queries were having over 40 parameters. However, this was not true in all the cases. There was an obvious failure in detecting the vulnerabilities in those projects that do not employ the defined matching pattern. By defining more and more patterns one may be able to achieve a detection and conversion rate of over 80%. However regular expressions cannot be used for those programs that employ complex logic inside the SQL query definition. For example, if a string builder was used to store the SQL query, with the query being added part by part, the matching pattern would be too difficult to write. In such situations analysis using the lexer and parser for dot net framework would provide accurate results.

SQL structure	Conversion
Static SQL	Yes
Dynamic SQL	Yes
Conditional SQL	Yes
Batch queries	No
Nested SQL	No

Table 1. The effectiveness of the developed conversion tool.

Nevertheless, this project showed the power of regular expressions in doing static analysis to prevent SQL injection vulnerability. If an organization needs to quickly convert all its code to parameterized queries a tool like this with regular expression patterns defined by comparing the organization's standard legacy code structure would be very useful.

Conclusion

In this paper, I described the SQL injection vulnerability and ways to mitigate the issue practically by exploiting the security benefits of parameterized queries. The paper described a tool that could assist the developer in successfully converting the SQL statements to parameterized queries with minimal manual intervention. This study though was done specifically focusing dotnet framework, but it is virtually applicable to all kinds of environments. Further, the study showed that such a tool carefully designed would be very helpful for the developer and can mitigate the SQL injection vulnerability to a large extent. 

Code for the Main tool Window (other dependency files excluded)